
This blog post is based on our paper accepted to International Conference on Learning Representations (ICLR) 2024. Please refer to the paper Tree Cross Attention for full details.
The Quest for Efficient Machine Learning Inference
In the fast-paced world of machine learning, one of the key goals is to make inference more efficient in terms of both computation and memory. It’s estimated that a whopping 80-90% of the machine learning workload comes from model inference, according to NVIDIA (Leopold, 2019) and Amazon (Barr, 2019). With the rise of low-memory compute domains such as IoT devices, problems with large context inputs (e.g., large language models), and the increasing popularity of attention based models, there’s a growing need to design more efficient attention mechanisms for performing inference.
Cross Attention (CA) is a well-known attention mechanism used at inference time to retrieve relevant information from a set of context inputs/tokens. However, CA scales linearly with the number of context tokens, making it unnecessarily expensive in practice as many of the context tokens are not needed. General-purpose architectures like Perceiver IO (Jaegle et al., 2021) offer a cheaper alternative by first distilling the contextual information into a smaller, fixed-size set of latent tokens. This makes the retrieval of information during inference more efficient.
However, methods that achieve efficient inference via latent modeling have their own set of challenges. For instance, problems with high intrinsic dimensionality naturally require a large number of latents. Additionally, the number of latents, which determines the capacity of the inference model, is a hyper parameter that needs to be specified before training. This can be problematic in many practical scenarios where the required model’s capacity may not be known beforehand. For example, in settings where the amount of data increases over time (like Bayesian Optimization, Contextual Bandits, Active Learning, etc.), the number of latents needed at the beginning and after many data acquisition steps can vary greatly.

Figure 1: Architecture Diagram of ReTreever. Input Array comprises a set of N context tokens which are fed through an encoder to compute a set of context encodings. Query Array denotes a batch of M query feature vectors. Tree Cross Attention organizes the encodings and constructs a tree T. At inference time, given a query feature vector, a logarithmic-sized subset of nodes (encodings) is retrieved from the tree T. The query feature vector retrieves information from the subset of encodings via Cross Attention and makes a prediction.
In this work, we introduce two novel ideas: Tree Cross Attention (TCA) and ReTreever. TCA is a proposed replacement for Cross Attention that performs retrieval, scaling logarithmically O(log(N)) with the number of context tokens. It organizes the tokens into a tree structure and performs retrieval via a tree search, starting from the root. This allows TCA to selectively choose the information to retrieve from the tree depending on a query feature vector. To learn good representations for the internal nodes of the tree, TCA leverages Reinforcement Learning (RL). Building on TCA, we also propose ReTreever, a flexible architecture that achieves token-efficient inference.
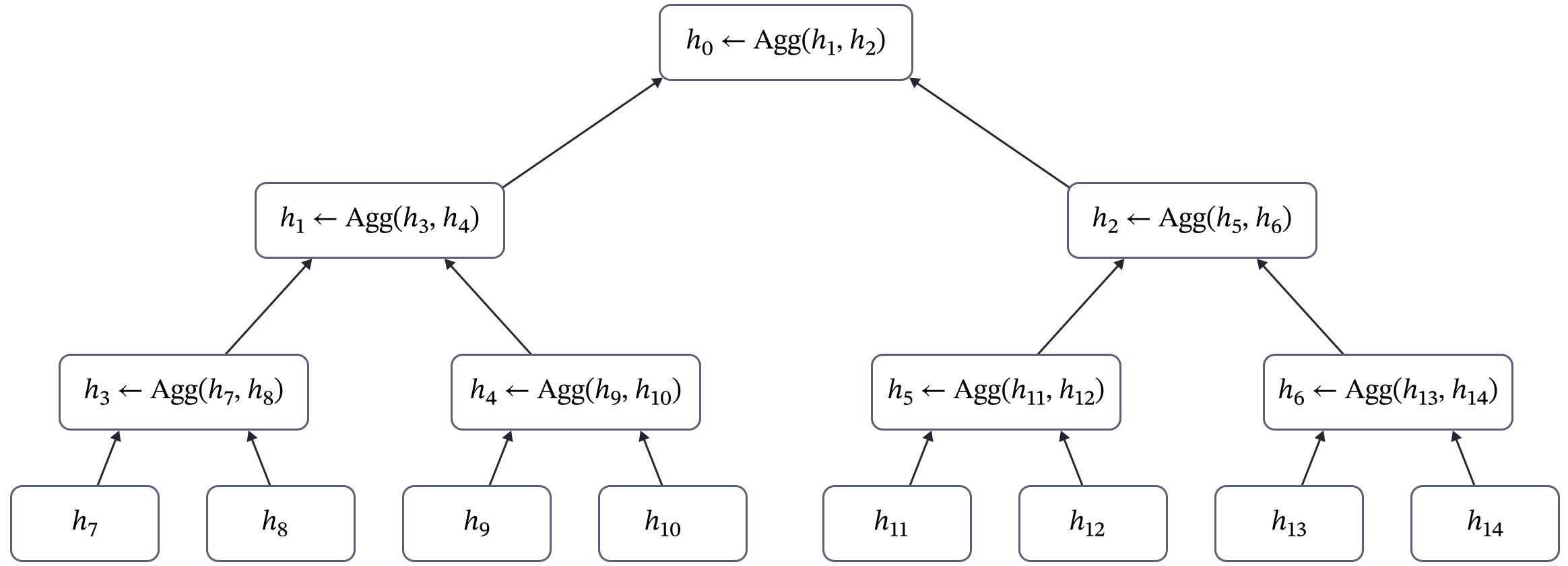
Figure 2: Diagram of the aggregation procedure performed during the Tree Construction phase. The aggregation procedure is performed bottom-up beginning from the parents of the leaves and ending at the root of the tree. The complexity of this procedure is O(N) but this only needs to be performed once for a set of context tokens. Compared to the cost of performing multiple predictions, the onetime cost of the aggregation process is minor.
Our experiments show that TCA achieves results competitive to that of Cross Attention while only requiring a logarithmic number of tokens. Furthermore, ReTreever outperforms Perceiver IO on various tasks while using the same number of tokens. Interestingly, ReTreever’s optimization objective can leverage non-differentiable objectives such as classification accuracy.
Unveiling Tree Cross Attention
Tree Cross Attention (TCA) is a more token-efficient version of Cross Attention, consisting of three main phases: Tree Construction, Retrieval, and Cross Attention.
In the Tree Construction phase, TCA arranges the context tokens into a tree structure. The context tokens become the leaves of the tree, and the internal nodes (the non-leaf nodes) summarize the information from their subtree. Importantly, this phase only needs to be done once for each set of context tokens.
The Retrieval and Cross Attention phases are performed multiple times during inference. In the Retrieval phase, the model selects a subset of nodes from the tree using a query feature vector. Then, in the Cross Attention phase, the model retrieves information from the selected nodes using the query feature vector. The overall complexity of inference is logarithmic per query feature vector, making it highly efficient.
Tree Construction
The tokens are organized into a tree where the leaves are all the tokens, and the internal nodes summarize the information of the nodes in their subtree. The information stored in a node has two specific purposes: making predictions and retrieval (finding the specific nodes in its subtree relevant for the query feature vector).
The method of organizing the data in the tree is flexible. It can be done with prior knowledge of the data structure, simple heuristics, or potentially learned. For example, we can use heuristics from traditional tree algorithms to organize the data, like ball-tree or k-d tree. After organizing the data in the tree, we use an aggregator function to aggregate the information of the tokens.
Starting from the parent nodes of the leaves of the tree, we perform the following aggregation procedure from the bottom up until we reach the root of the tree: each node represents the aggregation of its children nodes. This process is illustrated in Figure 2.
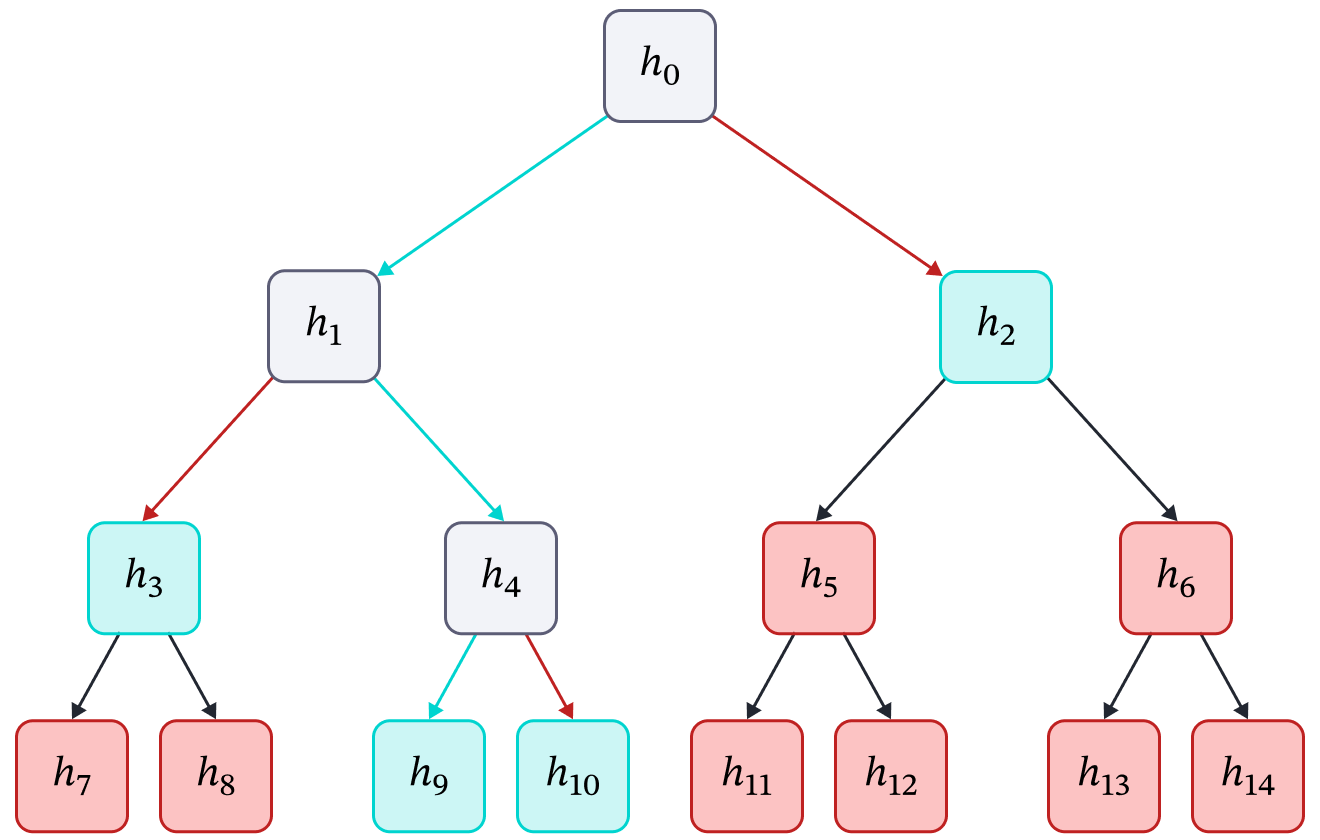
Figure 3: Example result of a Retrieval phase. The policy creates a path from the tree’s root to its leaves, selecting a subset of nodes: the terminal leaves in the path and the highest-level unexplored ancestors of the other leaves. The green arrows represent the path (actions) chosen by the policy π. The red arrows represent the actions rejected by the policy. The green nodes denote the subset of nodes selected, i.e., S = {h2, h3, h9, h10}. The grey nodes denote nodes that were explored at some point but not selected. The red nodes denote the nodes that were not explored or selected.
Retrieving Information
In this phase, we use a policy π learned via Reinforcement Learning to retrieve a subset of nodes from the tree. The process of retrieving the set of selected nodes S from the tree T is described in Figure 3 and Algorithm 1.
We start the search from the root of the tree. The policy’s state is the set of selected nodes S, the set of children nodes of the current node being explored Cv, and the query feature vector q. The policy selects one of the children nodes to further explore for more detailed information retrieval. The nodes that are not being further explored are added to the set of selected nodes. This process is repeated until we reach a leaf node, i.e., the search is complete. Since the height of a balanced tree is logarithmic, the number of nodes that are explored and retrieved is also logarithmic.
Require: Tree Structure ($\mathcal{T}$), policy ($\pi_\theta$), and query feature vector $q$
Ensure: Set of selected nodes ($\mathbb{S}$)
$\quad$$v \gets \mathrm{Root}(\mathcal{T})$
$\quad$$\mathbb{S} \gets \emptyset$
$\quad$while $v$ is not leaf do
$\qquad$$v’ \sim \pi_\theta( a | \mathbb{C}_v, q)$ where $a \in \mathbb{C}_v$
$\qquad$$\mathbb{S} \gets \mathbb{S} \cup (\mathbb{C}_v \backslash v’)$ $\qquad$$\mathbb{C}_v$ denotes children nodes of $v$
$\qquad$$v \gets v’$
$\quad$end while
$\quad$$\mathbb{S} \gets \mathbb{S} \cup v$
Applying Cross Attention
The set of nodes retrieved (S) is used as input for Cross Attention along with the query feature vector q. This results in a Cross Attention with overall logarithmic complexity per query feature vector. In contrast, applying Cross Attention to the full set of tokens has a linear complexity. Notably, the set of nodes S has a full receptive field of the entire set of tokens.
ReTreever: Efficient Retrieval with Tree Cross Attention
We’re excited to introduce ReTreever, a general-purpose model that achieves token-efficient inference by leveraging Tree Cross Attention. The architecture is similar to Perceiver IO’s, but with a key difference.
While Perceiver IO compresses information via a specialized encoder to achieve efficient inference, ReTreever’s inference is token-efficient irrespective of the encoder, scaling logarithmically with the number of tokens. This means the choice of encoder is flexible and can be, for example, a Transformer Encoder or efficient versions such as Linformer, ChordMixer, etc.
Training ReTreever
The training objective of ReTreever consists of three components, each with its own purpose and weight in the overall objective:
$$
\mathcal{L}_{ReTreever} = \mathcal{L}_{TCA} + \lambda_{RL} \mathcal{L}_{RL} + \lambda_{CA} \mathcal{L}_{CA}
$$
$\mathcal{L}_{TCA}$ is designed to learn node representations in the tree that summarize the relevant information in its subtree for making good predictions.
$$
\mathcal{L}_{TCA} = \mathrm{Loss}(\mathrm{CrossAttention}(x, \mathbb{S}), y)
$$
$\mathcal{L}_{RL}$ is used to learn internal node representations for retrieval within the tree structure.
$$\mathcal{L}_{RL} = \sum_{t=0}^{\log(N) – 1} \left[ \mathcal{R} \log \pi_\theta (a_t | s_t) + \alpha \mathcal{H}[\pi_\theta(\cdot | s_t)] \right]$$
Here, $\mathcal{R}$ denotes the reward we want ReTreever to maximize. This reward typically corresponds to the negative TCA loss $\mathcal{R} = -\mathcal{L}_{TCA}$. However, crucially, the reward does not need to be differentiable. As such, $\mathcal{R}$ can also be an objective we are typically not able to optimize directly via gradient descent.
Lastly, $\mathcal{L}_{CA}$ is included to improve the early stages of training and encourage TCA to learn good node representations.
$$
\mathcal{L}_{CA} = \mathrm{Loss}(\mathrm{CrossAttention}(x, \mathrm{Leaves(\mathcal{T})}), y)
$$
TCA and ReTreever Experiments
Comparing Tree Cross Attention with Cross Attention
We begin by verifying Tree Cross Attention (TCA)’s ability to perform retrieval. The models are provided with a sequence of length $N=2^k$, beginning with a [BOS] (Beginning of Sequence) token, followed by a randomly generated palindrome comprising of $2^{k}-2$ digits, ending with a [EOS] (End of Sequence) token. The objective of the task is to predict the second half ($2^{k-1}$) of the sequence given the first half ($2^{k-1}$ tokens) of the sequence as context.
Results. Tree Cross Attention was able to solve this task perfectly (Table 1). In contrast with Cross Attention, TCA performs tree-based memory retrieval, selectively retrieving a small subset of tokens for predictions. As such, TCA is able to solve the task perfectly while requiring $\sim 50 \times$ fewer tokens than Cross Attention.
| Method | $N=256$ | $N=512$ | $N=1024$ | |||
|---|---|---|---|---|---|---|
| $\%$ Tokens | Accuracy | $\%$ Tokens | Accuracy | $\%$ Tokens | Accuracy | |
| Cross Attention TCA | $100.0\%$ $\mathbf{6.3\%}$ | $\mathbf{100.0 \pm 0.0}$ $\mathbf{100.0 \pm 0.0}$ | $100.0\%$ $\mathbf{3.5\%}$ | $\mathbf{100.0 \pm 0.0}$ $\mathbf{100.0 \pm 0.0}$ | $100.0\%$ $\mathbf{2.0\%}$ | $\mathbf{99.9 \pm 0.2}$ $\mathbf{99.6 \pm 0.6}$ |
Comparing ReTreever with Perceiver IO
We evaluated ReTreever on popular uncertainty estimation settings used in (Conditional) Neural Processes literature and which have been benchmarked extensively (Garnelo et al., 2018a;b; Kim et al., 2019; Lee et al., 2020; Nguyen & Grover, 2022; Feng et al., 2023a;b). As a reference, we also compare with a strong baseline Transformer + Cross Attention which uses all the tokens for predictions. We refer the reader to the paper for full results.
Results. In Table 2, we see that ReTreever outperforms Perceiver IO significantly on both CelebA and EMNIST while using the same number of tokens. Compared with Transformer + Cross Attention, ReTreever uses $\sim 21 \times$ fewer tokens, making it significantly more token-efficient.
| Method | CelebA | EMNIST | ||
|---|---|---|---|---|
| $\%$ Tokens | LogLikelihood | $\%$ Tokens | LogLikelihood | |
| Transformer + Cross Attention Perceiver IO ReTreever | $100.0\%$ $\mathbf{4.6\%}$ $\mathbf{4.6\%}$ | $\mathbf{3.88 \pm 0.01}$ $3.20 \pm 0.01$ $3.52 \pm 0.01$ | $100.0\%$ $\mathbf{4.6\%}$ $\mathbf{4.6\%}$ | $\mathbf{1.41 \pm 0.00}$ $1.25 \pm 0.01$ $1.30 \pm 0.01$ |
Optimising non-differentiable objectives using $\mathcal{L}_{RL}$.
In deep learning, we often use cross entropy instead of accuracy during the gradient descent optimization since it is differentiable. However, TCA leverages RL which does not require its objective to be differentiable. As such, we compare the performance of TCA when optimizing for accuracy and negative cross entropy.
Results. Table 3 shows that accuracy is better than negative cross entropy as the RL reward. This is not surprising since (1) the metric we evaluate our model on is accuracy and not cross entropy, and (2) accuracy as a reward is simpler compared to negative cross entropy as a reward, making it easier for a policy to optimize. More specifically, a reward using accuracy as the metric is either: $\mathcal{R} = 0$ for an incorrect prediction or $\mathcal{R} = 1$ for a correct prediction. However, a reward based on cross entropy can have vastly different values for incorrect predictions.
| Method | $N=256$ | $N=512$ | $N=1024$ | |||
|---|---|---|---|---|---|---|
| $\%$ Tokens | Accuracy | $\%$ Tokens | Accuracy | $\%$ Tokens | Accuracy | |
| TCA (Acc) TCA (Neg. CE) | $\mathbf{6.3\%}$ $\mathbf{6.3\%}$ | $\mathbf{100.0 \pm 0.0}$ $\mathbf{99.8 \pm 0.3}$ | $\mathbf{3.5\%}$ $\mathbf{3.5\%}$ | $\mathbf{100.0 \pm 0.0}$ $95.5 \pm 3.8$ | $\mathbf{2.0\%}$ $\mathbf{2.0\%}$ | $\mathbf{99.6 \pm 0.6}$ $80.3 \pm 14.8$ |
Conclusion
In this work, we proposed Tree Cross Attention (TCA), a variant of Cross Attention that only requires a logarithmic $\mathcal{O}(\log(N))$ number of tokens when performing inferences. By leveraging RL, TCA can optimize non-differentiable objectives. Building on TCA, we introduced ReTreever, a flexible architecture for token-efficient inference. Empirically, we show that (1) TCA achieves performance comparable to Cross Attention while being significantly more token efficient and (2) ReTreever outperforms Perceiver IO while using the same number of tokens.
References
Jeff Barr. Amazon ec2 update – inf1 instances with aws inferentia chips for high performance cost-effective inferencing, Dec 2019.
Leo Feng, Hossein Hajimirsadeghi, Yoshua Bengio, and Mohamed Osama Ahmed. Latent bottlenecked attentive neural processes. In International Conference on Learning Representations, 2023a.
Leo Feng, Frederick Tung, Hossein Hajimirsadeghi, Yoshua Bengio, and Mohamed Osama Ahmed. Memory efficient neural processes via constant memory attention block. arXiv preprint arXiv:2305.14567, 2023b.
Marta Garnelo, Dan Rosenbaum, Christopher Maddison, Tiago Ramalho, David Saxton, Murray Shanahan, Yee Whye Teh, Danilo Rezende, and SM Ali Eslami. Conditional neural processes. In International Conference on Machine Learning, pp. 1704–1713. PMLR, 2018a.
Marta Garnelo, Jonathan Schwarz, Dan Rosenbaum, Fabio Viola, Danilo J Rezende, SM Eslami, and Yee Whye Teh. Neural processes. arXiv preprint arXiv:1807.01622, 2018b.
Andrew Jaegle, Sebastian Borgeaud, Jean-Baptiste Alayrac, Carl Doersch, Catalin Ionescu, David Ding, Skanda Koppula, Daniel Zoran, Andrew Brock, Evan Shelhamer, et al. Perceiver io: A general architecture for structured inputs & outputs. In International Conference on Learning Representations, 2021.
Hyunjik Kim, Andriy Mnih, Jonathan Schwarz, Marta Garnelo, Ali Eslami, Dan Rosenbaum, Oriol Vinyals, and Yee Whye Teh. Attentive neural processes. 2019.
Juho Lee, Yoonho Lee, Jungtaek Kim, Eunho Yang, Sung Ju Hwang, and Yee Whye Teh. Bootstrapping neural processes. Advances in neural information processing systems, 33:6606–6615, 2020.
George Leopold. Aws to offer nvidia’s t4 gpus for ai inferencing, Mar 2019.
Tung Nguyen and Aditya Grover. Transformer neural processes: Uncertainty-aware meta learning via sequence modeling. In International Conference on Machine Learning, pp. 16569–16594. PMLR, 2022.
Work with us!
Impressed by the work of the team? RBC Borealis is looking to hire for various roles across different teams. Visit our career page now to find the right role for you and join our team!
View open roles