
A Deep Dive into the ICLR 2025 Breakthrough
Introduction
Transformer models have revolutionized various domains, from natural language processing to image classification. However, their core dot-product attention mechanism scales quadratically with the sequence length, posing severe challenges for long-context data. Radar, introduced in the ICLR 2025 paper [1], offers a training-free solution that accelerates inference by dynamically retrieving the most important tokens. This blog post provides an in-depth look into Radar, its algorithmic innovations, and how it balances speed and quality in long-context decoding.
Motivation and Background
The Challenges with Long-Context Decoding

Figure 1: An illustration of the standard dot-product attention with one query token $q$.
The standard dot-product attention (shown in Figure 1) computes pairwise interactions among all keys $k_1, \dots, k_t$ and the query $q_t$ for every query at $t = 1 \dots T$, leading to an overall quadratic time complexity: $O(T^2)$, where ( T ) is the number of tokens. As sequences grow longer (e.g., legal documents, lengthy code files), this quadratic scaling becomes a critical bottleneck, both in terms of computational resources and latency.
Previous efforts to address this issue include sparse attention mechanisms [2, 3] and kernelized attention approximations [4]. However, these methods typically require additional training or sacrifice information by heuristically evicting tokens.
Radar: A Training-Free Approach
Radar is unique in that it:
- Operates without training: It works on any pre-trained Transformer without additional parameter tuning.
- Maintains long-context information: Unlike methods that evict tokens, Radar dynamically searches for and utilizes the most critical tokens.
- Reduces time complexity: By exploiting a hierarchical segmentation and random projection technique, Radar reduces overall complexity to \( O(\sqrt{t}) \) per generated token (or $O(t^{1.5})$ for all $t$ tokens).
Methodology
Hierarchical Structure and Random Projections
As illustrated in Figure 2, Radar employs a hierarchical structure to represent the context:
- Bottom Layer: Contains individual token key embeddings.
- Top Layer: Consists of segments—groups of tokens—each summarized by averaging their random projections.
For a given token key \( k \in \mathbb{R}^d \), Radar applies a random projection defined as:
\begin{equation}
\phi_\Omega(k) = \frac{1}{\sqrt{n}} \left( \exp\left(\omega_1^\top k’ – \frac{|| k’ ||_2^2}{2}\right), \dots, \exp\left(\omega_n^\top k’ – \frac{|| k’ ||_2^2}{2}\right) \right),
\label{eq:randomprojection}
\tag{1}
\end{equation}
where \( k’ = \frac{k}{d^{1/4}} \) and \( \Omega \in \mathbb{R}^{n \times d} \) with rows \( \omega_i \) sampled from \( \mathcal{N}(0,1) \). The segment embedding is then computed as:
\begin{equation}
\bar{\phi}_\Omega(k_{i:i+c}) = \frac{1}{c} \sum_{l=0}^{c-1} \phi_\Omega(k_{i+l}).
\label{eq:segment_embedding}
\tag{2}
\end{equation}
Radar saves these segment embeddings, which are later used for querying.
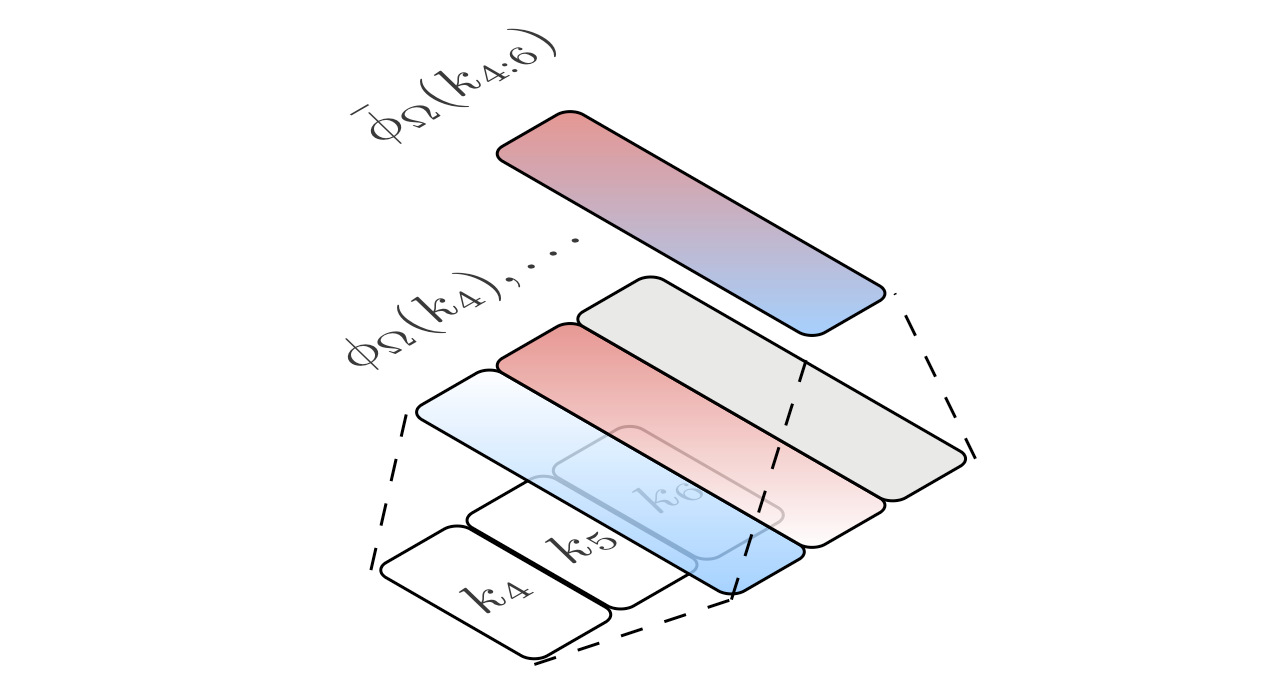
(a) Construction process for a single segment consists of three tokens $k_{4:6}$. Each token embedding is mapped to the random feature $\phi_\Omega(k_i)$. The segment embedding $\bar\phi_\Omega(k_{4:6})$ is then the average of random features.

(b) Query process for a single query $q$. The query token is first mapped to the random feature $\phi_\Omega(q)$. The segment importance is obtained by inner products between random features $\phi_\Omega^\top(q)\bar\phi_\Omega(k_{i:i+2})$. In this example, the second segment has the highest (unnormalized) segment attention of $2.2$.
Accelerated Segment Search
During decoding with a query vector $q$, Radar first evaluates the importance of each segment by computing the inner product between the query’s projected feature and the segment embeddings:
\begin{equation}
\text{score}(l) = \phi_\Omega(q)^\top \bar{\phi}_\Omega(k_{l:l+c}),
\label{eq:segment_score}
\tag{3}
\end{equation}
and then selects the top-\( k \) segments that maximize this score. By doing so, the attention computation for each query is performed only on a subset of tokens, thereby reducing the complexity. This score is theoretically justified.
Dynamic Restructuring
As the sequence length grows, Radar adapts the segment length \( c \) dynamically such that \( c = O(\sqrt{t}) \). This dynamic restructuring is executed only when \( \sqrt{t} \) is an integer, ensuring that the amortized cost remains low. For other steps, a sliding window buffer is maintained, preserving context without incurring the full cost of re-segmentation.
Theoretical Justifications
Radar is underpinned by rigorous theoretical guarantees. The basis for using random projections to approximate the attention mechanism is inspired by previous work [4], which shows:
Lemma 1 (Projection Soundness). For any \( u, v \in \mathbb{R}^d \), with the mapping defined in Equation 1, we have:
\[
\mathbb{E}_\Omega[\phi_\Omega(u)^\top \phi_\Omega(v)] = \exp\left(\frac{u^\top v}{\sqrt{d}}\right).
\]
Based on the lemma, Radar has the following guarantee:
Theorem 2 (Correctness of Radar). Let each segment consist of \( c \) tokens. Assume that the first segment \( k_{1:1+c} \) has the highest attention score with respect to the query \( q \). With probability at least \( 1-\delta \), we have:
\[
\phi_\Omega(q)^\top \bar{\phi}_\Omega(k_{1:c+1}) = \max_{l} \phi_\Omega(q)^\top \bar{\phi}_\Omega(k_{l:l+c}),
\]
provided that the minimum gap between the best segment and the others satisfies a condition proportional to
\[
\frac{1}{c}\exp\left(\frac{\zeta^2}{\sqrt{d}}\right) \sqrt{\frac{8\log(2(c-1)/\delta)}{n}},
\]
where \( \zeta \) is the maximum norm among the key tokens and \( q \) [1].
The above theorem ensures that Radar’s approximation reliably identifies the segments with the highest attention scores, even with reduced computation.
Experimental Evaluation
Radar’s performance was extensively validated on diverse tasks, including language modeling and code generation. The experiments compared Radar with several baselines such as vanilla dot-product attention and StreamingLLM.
Long-Context Perplexity
One of the key evaluations involved measuring the perplexity on long-context datasets (e.g., PG-19 and The Stack). Figure 3 summarizes the performance comparison.

Figure 3: Comparison of perplexity and elapsed time across different models. Radar maintains a perplexity close to the vanilla attention while achieving over 2x speed-up. (Caption: Performance on Long-Context Tasks)
Benchmarking on LongBench
Radar was also evaluated on the LongBench benchmark, covering multiple tasks such as single-document QA, summarization, and code generation. The following table (Table 1) provides an overview of the average performance metrics.
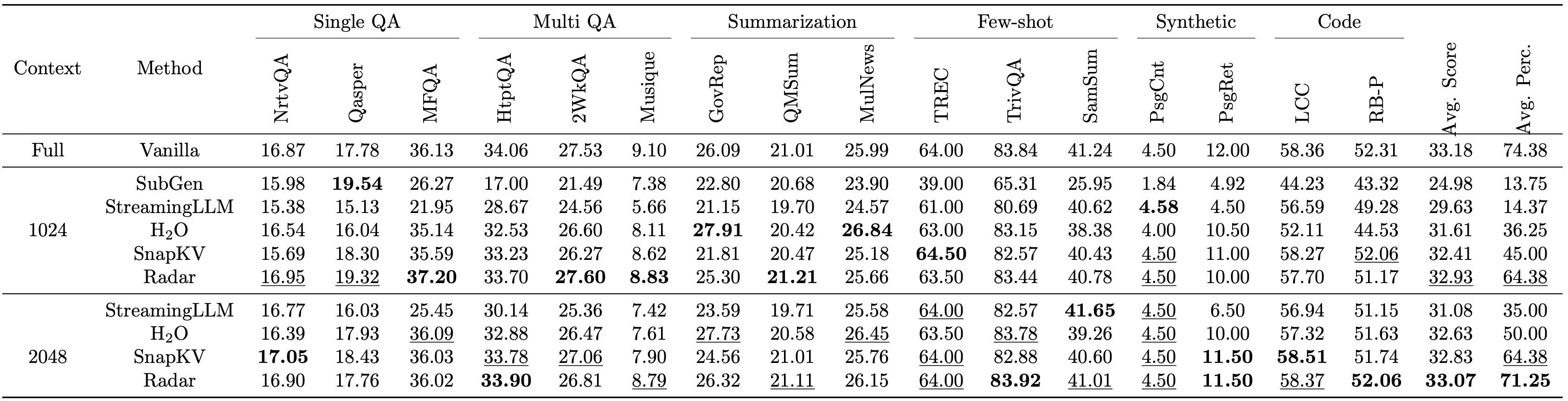
Table 1: The LongBench benchmark results of different methods applied on Llama-2-7b-chat-hf. Each prompt contains maximum 3.5K tokens as the model can handle maximum 4K tokens.
As shown, Radar achieves the highest average scores and average percentiles across all $n_c$ settings. Notably, Radar with 1024 middle tokens outperforms SnapKV with 2048 middle tokens in terms of average score. The results strongly suggest the effectiveness of our method in utilizing the context.
Ablation Studies and Hyper-Parameter Effects
Radar introduces two key hyper-parameters: the projection dimension \( n \) and the number of selected segments \( k \). Ablation studies reveal that:
- Increasing \( n \) improves the attention approximation, leading to better generation quality.
- Increasing \( k \) results in higher quality at the expense of increased memory usage.
Figures 4a and 4b illustrate these trade-offs.
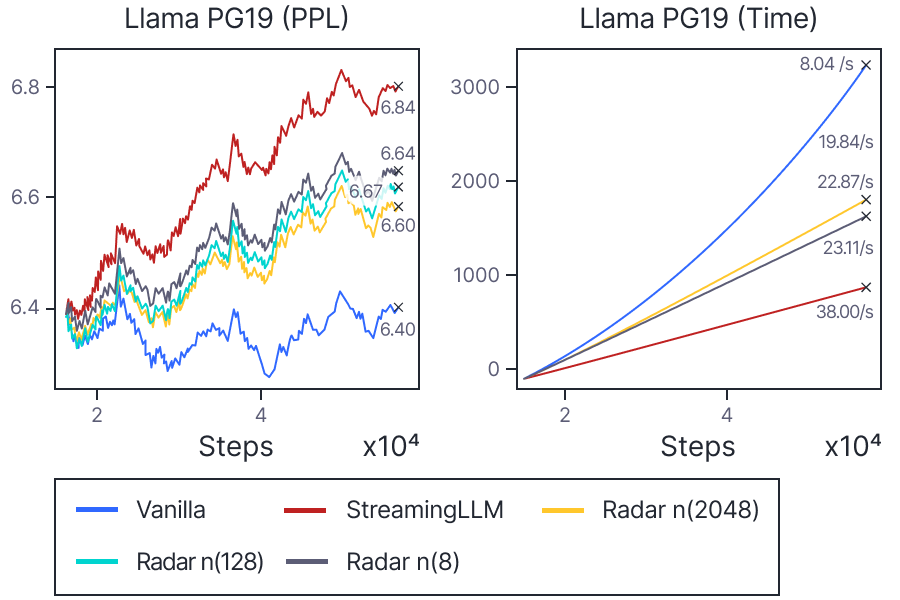
Figure 4. (a) The effect of the projection dimension \( n \) on generation quality. Higher \( n \) provides a closer approximation to full attention.

Figure 4. (b) The effect of the number of selected segments \( k \). An increase in \( k \) improves quality while increasing computational overhead.
Discussion and Future Directions
Radar represents a significant advancement in long-context processing for Transformer models. By leveraging a hierarchical segmentation strategy combined with random feature approximations, Radar reduces the inference complexity from quadratic to \( O(t^{1.5}) \) without requiring retraining of the model. This opens the door for applying large pre-trained models to tasks such as legal document analysis and code generation where long contexts are inevitable.
Future research may explore:
- Adaptive Buffering: Further refining the dynamic restructuring mechanism for even lower overhead.
- Integration with Other Techniques: Combining Radar with memory-efficient attention methods such as FlashAttention [5] for additional speed-ups.
- Broader Applications: Extending the approach to multimodal tasks where context length is similarly problematic.
Conclusion
Radar stands out as a training-free, efficient alternative for long-context inference in Transformer models. Its innovative use of random projections and dynamic segmentation not only preserves critical information from long contexts but also ensures that computational complexity remains manageable. With strong theoretical guarantees [1] and extensive empirical validation, Radar is poised to make long-context applications more practical and efficient.
References
[1] Yongchang Hao, Mengyao Zhai, Hossein Hajimirsadeghi, Sepidehsadat Hosseini, and Frederick Tung.
Radar: Fast long-context decoding for any transformer. In The Thirteenth International Conference on
Learning Representations, 2025.
[2] Rewon Child, Scott Gray, Alec Radford, and Ilya Sutskever. Generating long sequences with sparse
transformers. arXiv preprint arXiv:1904.10509, 2019.
[3] Iz Beltagy, Matthew E. Peters, and Arman Cohan. Longformer: The long-document transformer.
arXiv:2004.05150, 2020.
[4] Krzysztof Marcin Choromanski, Valerii Likhosherstov, David Dohan, Xingyou Song, Andreea Gane,
Tamas Sarlos, Peter Hawkins, Jared Quincy Davis, Afroz Mohiuddin, Lukasz Kaiser, David Benjamin
Belanger, Lucy J Colwell, and Adrian Weller. Rethinking attention with performers. In ICLR, 2021.
[5] Tri Dao, Dan Fu, Stefano Ermon, Atri Rudra, and Christopher R´e. FlashAttention: Fast and memory-efficient exact attention with IO-awareness. NeurIPS, 35:16344–16359, 2022.