
This blog post is based on our ICLR2023 paper; please refer to the Scaleformer: Iterative Multi-scale Refining Transformers for Time Series Forecasting paper for full details. Our code is publicly available in Scaleformer – GitHub.
Time-series forecasting plays an important role in many domains, including weather forecasting, inventory planning, astronomy, and economic and financial forecasting. At RBC Borealis, we are interested in improving real-world time-series data modelling, with applications to both financial datasets and personal banking.
While transformer-based architectures have become the mainstream and state-of-the-art for time series forecasting in recent years, advances have focused mainly on mitigating the standard quadratic complexity in time and space, through structural changes [1,2] or alterations to the attention mechanism [3,4], rather than by introducing explicit scale-awareness. As a result, the essential cross-scale feature relationships are often learnt implicitly and are not encouraged by architectural priors of any kind beyond the stacked attention blocks that characterize the transformer models. Autoformer [1] and Fedformer [2] introduced some emphasis on scale-awareness by enforcing different computational paths for the trend and seasonal components of the input time series; however, this structural prior only focused on two scales: low- and high-frequency components.
Given their importance to forecasting, can we make transformers more scale-aware?
We propose to address this question with Scaleformer. In our proposed approach, showcased in Figure 1, time series forecasts are iteratively refined at successive time-steps, allowing the model to better capture the inter-dependencies and specificities of each scale. However, iterative refinement itself is not sufficient as it can cause significant distribution shifts between intermediate forecasts leading to runaway error propagation. To mitigate this issue, we introduce cross-scale normalization at each step.
Our approach reorders model capacity to shift the focus on scale awareness but does not fundamentally alter the attention-driven paradigm of transformers. As a result, it can be readily adapted to work jointly with multiple recent time series transformer architectures, acting broadly orthogonally to their own contributions. Leveraging this, we chose to operate with various transformer-based backbones (e.g. Fedformer, Autoformer, Informer, Reformer, Performer) to further probe the effect of our multi-scale method on a variety of experimental setups.
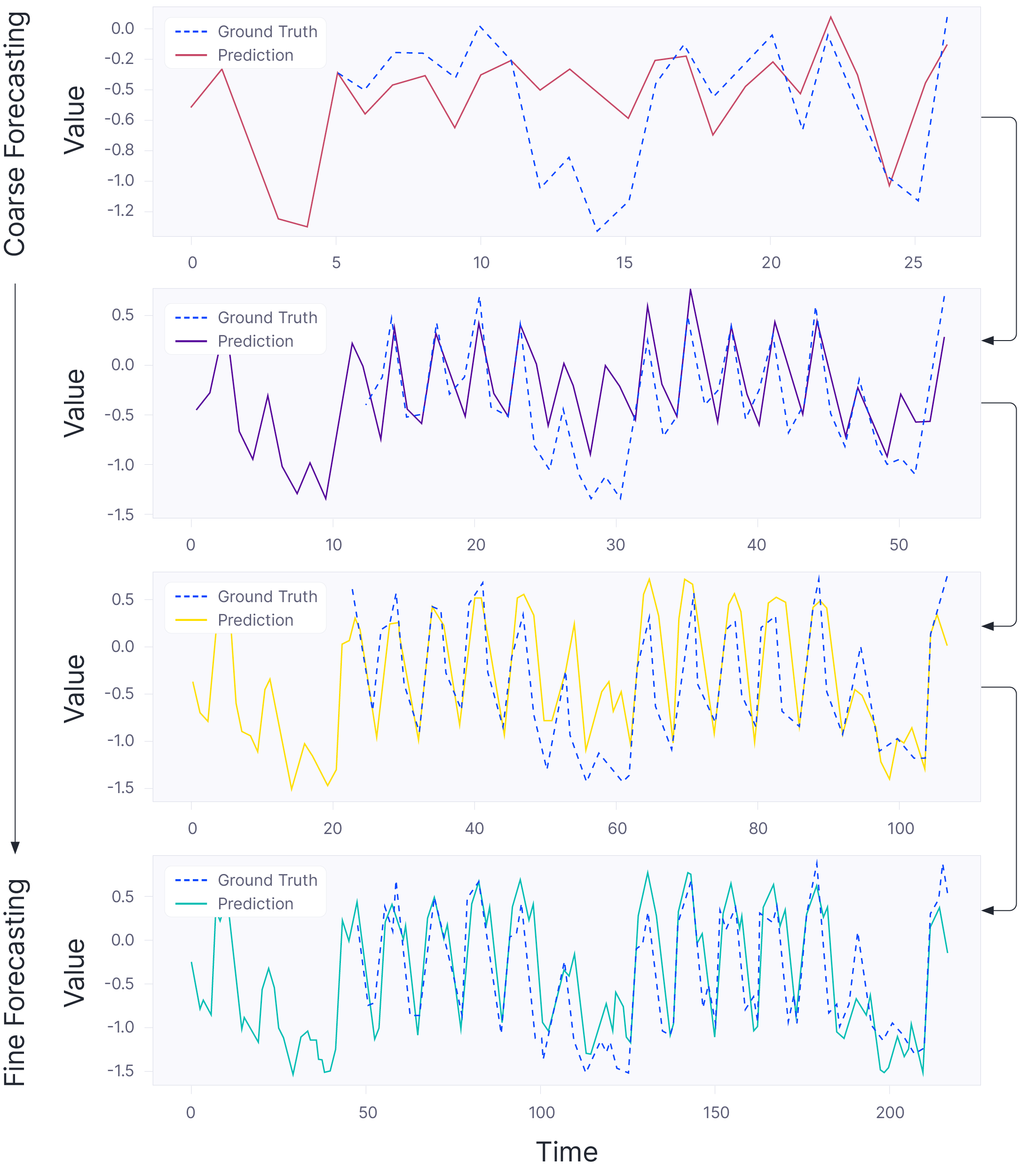
Figure 1: Intermediate forecasts by our model at different time scales. Iterative refinement of a time series forecast is a strong structural prior that benefits time series forecasting.
Our Method
Altering transformers to better account for scale is a complicate process, which requires a number of architectural and methodological changes to yield strong benefits.
Multi-scale Framework
Our proposed framework applies successive transformer modules to iteratively refine a time-series forecast, at different temporal scales. The proposed framework is shown in Figure 2. Please refer to our paper for more details.
Cross-scale Normalization
Training time-series forecasting models typically suffers from distribution shifts between train and evaluation sets [5,6], as well as between the horizon and forecast windows. Iterative refinement adds a third issue: distribution shifts between internal representations at different scales. Normalizing the output at a given step by either the look-back window statistics or the previously predicted forecast window statistics results in an accumulation of errors across steps. We mitigate this by considering a moving average of forecast and look-back statistics as the basis for the output normalization. While this change might appear relatively minor, it has a significant impact on the resulting distribution of outputs.
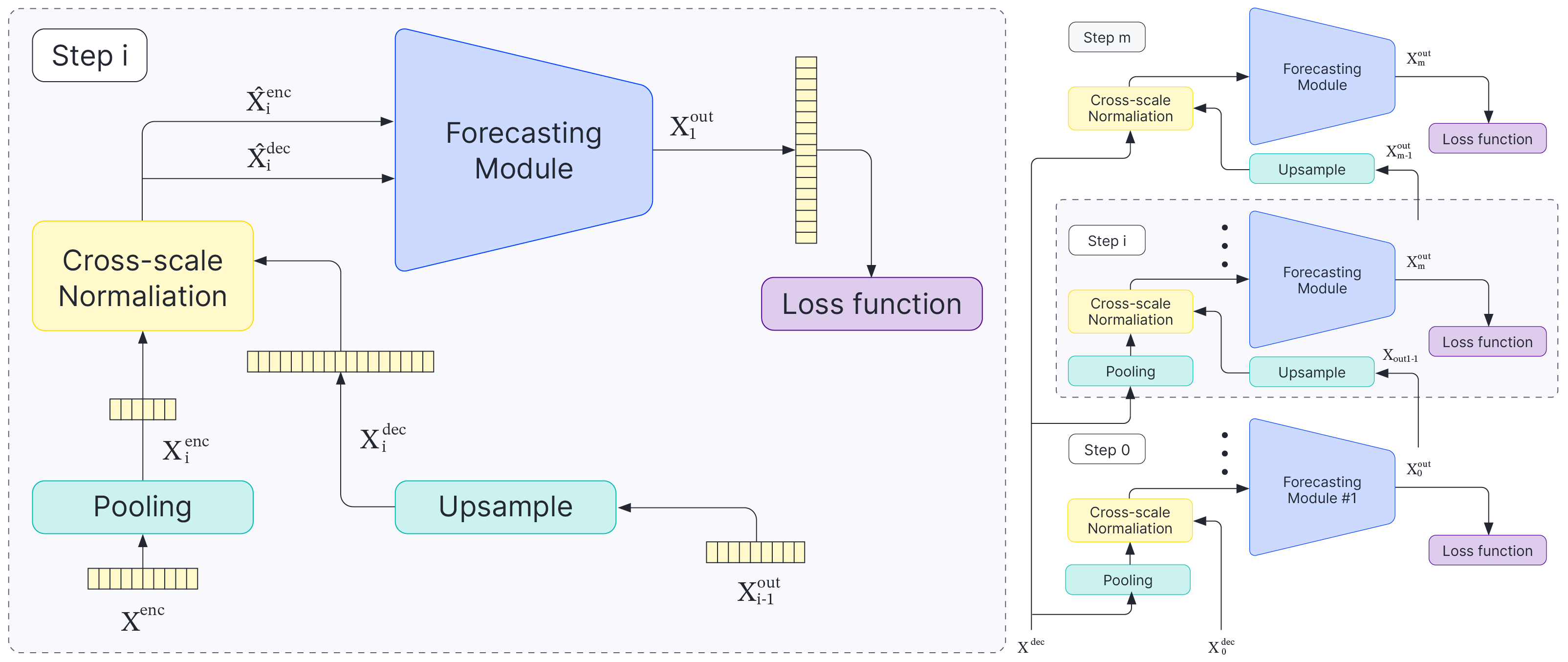
Figure 2: Overview of the proposed Scaleformer framework. (Left) Representation of a single scale block. In each step, we pass the normalized upsampled output from the previous step along with the normalized downsampled encoder as the input. (Right) Representation of the full architecture. We process the input in a multi-scale manner iteratively from the smallest scale to the original scale.
Loss Function
Using the standard MSE objective to train time-series forecasting models leaves them sensitive to outliers. This is amplified by iterative refinement, which leads to a compounding of errors. One possible solution is to use objectives more robust to outliers, such as the Huber loss [7]. However, when there are no major outliers, such objectives tend to underperform. One of our contributions is to replace the standard learning objective with a variation of an adaptive training objective initially used in computer vision [8]. This objective, mitigates outlier sensitivity while retaining good performance in situations where there are fewer outliers.
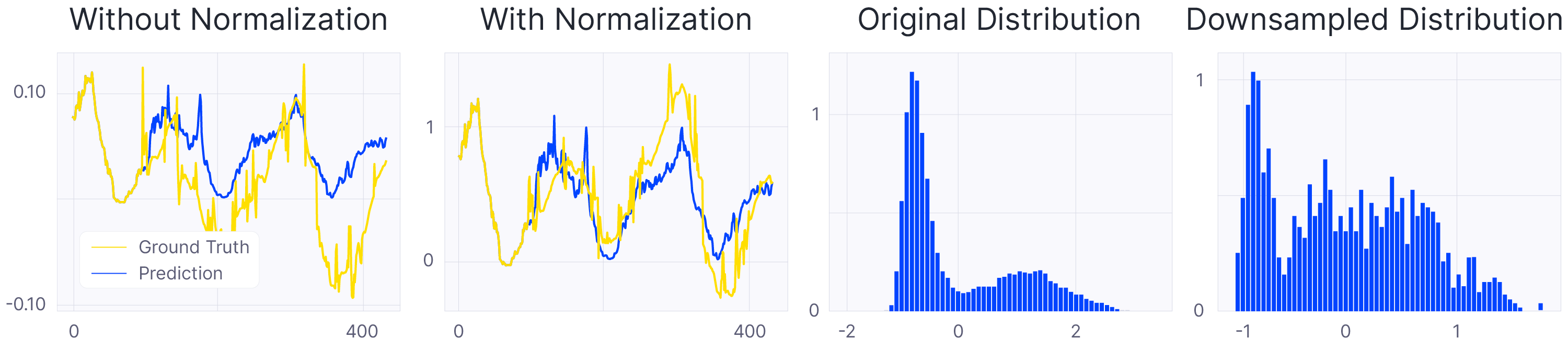
Figure 3: The figure shows the output results of two series using the same trained multi-scale model with and without shifting the data (left) which demonstrates the importance of normalization. On the right, we can see the distribution changes due to the downsampling of two series compared to the original scales from the Electricity dataset.
| Method | FEDformer-MSA | FEDformer-MSA | Autoformer-MSA | Autoformer-MSA | Informer-MSA | Informer-MSA | Reformer-MSA | Reformer-MSA | Performer-MSA | Performer-MSA |
| Metric | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE |
| Vs Ours | 5.6% | 5.9% | 13.5% | 9.1% | 38.5% | 26.7% | 38.3% | 25.2% | 23.3% | 16.9% |
Table 1: Comparison of the MSE and MAE results for our proposed multi-scale framework version of different methods (-MSA) with respective baselines. The average improvement (error reduction) is shown with respect to the base models.
Main Results
The proposed framework results in strong improvements over a diverse set of baselines. Table [1] highlights the relative gains Scaleformer provides over a set of non-scale-aware baselines. The baselines cover most of the recent transformer-based approaches to forecasting, demonstrating the robustness of the proposed changes. Depending on the choice of transformer architecture, our multi-scale framework results in mean squared error reductions ranging from 5.5% to 38.5%. We also validate the use of both the adaptive loss and the multi-scale framework itself. Please refer to our paper for more details.
Moving Forward
The Scaleformer structural prior has been shown to be beneficial when applied to transformer-based, deterministic time series forecasting. It is not however limited to those settings. The results showed in our paper demonstrate that Scaleformer can adapt to settings distinct from point-wise time-series forecasts with transformers (the primary scope of our paper), such as probabilistic forecasts and non-transformer models, such as N-Beats [9]. We consider such directions to therefore be promising for future work.
As we have seen, scale-aware models perform well, in a wide variety of settings. More generally, this work highlights the strong impact of simple structural priors in time-series forecasting. Going forward, our research team aims to keep investigating related questions, both related to better understanding such priors through more analysis, and developing new ones. If you are interested in this topic, or related ones, we would be happy to hear from you!
References
[1] J. Xu, J. Wang, M. Long, et al., “Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting,” Advances in Neural Information Processing Systems, vol. 34, 2021.
[2] T. Zhou, Z. Ma, Q. Wen, X. Wang, L. Sun, and R. Jin, “FEDformer: Frequency enhanced decomposed transformer for long-term forecasting,” in Proc. 39th International Conference on Machine Learning (ICML 2022), 2022.
[3] S. Li, X. Jin, Y. Xuan, X. Zhou, W. Chen, Y.-X. Wang, and X. Yan, “Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting,” Advances in Neural Information Processing Systems, vol. 32, pp. 5243-5253, 2019.
[4] H. Zhou, S. Zhang, J. Peng, S. Zhang, J. Li, H. Xiong, and W. Zhang, “Informer: Beyond efficient transformer for long sequence time-series forecasting,” in Proceedings of AAAI, 2021
[5] H. Shimodaira, “Improving predictive inference under covariate shift by weighting the log-likelihood function,” Journal of statistical planning and inference, vol 90, no. 2, pp. 227-244, 2000.
[6] S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in International conference on machine learning, pp. 488-456, PMLR, 2015.
[7] P.J. Huber, “Robust Estimation of a Location Parameter,” The Annals of Mathematical Statistics, vol. 35, no. 1, pp. 73 – 101, 1964.
[8] J.T. Barron, “A general and adaptive robust loss function,” in Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 4331 – 4339, 2019.
[ 9 ] B. N. Oreshkin, D. Carpov, N. Chapados, and Y. Bengio, “N-beats: Neural basis expansion analysis for interpretable time series forecasting, ” in International Conference on Learning Representations, 2020.